
|
ЕГЭ МАТЕМАТИКА 2017
ДЕМО
Профильный уровень
ПРОДОЛЖЕНИЕ
.gif) Начало здесь Начало здесь
|
|
|
Найдите  |
|
|
Все мы прекрасно знаем основное тригонометрическое тождество

Отсюда мы легко найдём синус альфа

Но при извлечении квадратного корня может быть как положительное, так и отрицательное число. Какое же взять? На это указывает условие - в каком промежутке лежит угол альфа.
Вспомним, тригонометрический круг

От пи до двух пи синус отрицательный. Поэтому для ответа выберем отрицательное число - 0,8.
Нам по условию требуется найти синус двойного угла. Вспомним формулу

Подставляем в эту формулу данный в задании косинус и только что вычисленный синус, получаем
2 х (-0,8) х 0,6 = -0,96
|
|
|
-0,96 |
|
|
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением

где c = 1500 м/с — скорость звука в воде; f0 — частота испускаемого сигнала (в МГц); f — частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.
|
|
|
Лучше всего сразу подставить в исходную формулу числовые значения

Получилось обычное уравнение с одним неизвестным f, которое и надо решить

|
|
|
751 |
|
|
Весной катер идёт против течения реки в 1 и 2/3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1 и1/2 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч). |
|
|
Задание проверяет наше умение строить алгебраические модели реальных ситуаций. Обычно надо на основе заданных условий составить уравнение или систему уравнений, а потом решить их.
Пусть у - скорость катера в стоячей воде.
Пусть х - скорость течения реки весной.
Тогда, по условию, (х - 1) - скорость течения реки летом.
Тогда весной
у - х скорость катера против течения;
у + х скорость катера по течению.
И в условии сказано, что

А летом
у - (х - 1) = у - х + 1 скорость катера против течения;
у + х - 1 скорость катера по течению.
В условии сказано, что

В последнее выражение подставим у = 4 х, кторое мы нашли из условия движения катера весной

|
|
|
5 |
|
|
Найдите точку максимума функции  |
|
|
Помнишь, мы рассматривали возрастающую, убывающую и перегибающуюся с возрастания на убывание функцию? Это было в задаче 7. Мы говорили, что при возрастании функции её производная имеет знак "плюс", при убывании "минус", а в точке перегиба производная равна нулю.
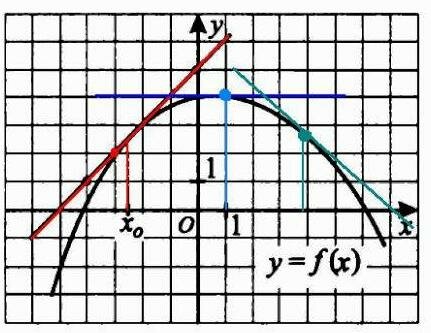
А ведь точка перегиба - это и есть точка МАКСИМУМА функции. Именно в точке перегиба функция У имеет наибольшее значение! (По правде сказать, может быть и минимум, но об этом позднее).
Таким образом, решать задачу будем в два действия: 1) Найдём производную от функции 2) Приравняем производную к нулю и решим полученное уравнение.
1) Находим производную. Во-первых, помним, что производная суммы равна сумме производных.

Производная от второго слагаемого, от 2х, равна просто 2; производная от третьего слагаемого, от 7, вообще равна нулю. А вот первое слагаемое - это сложная функция и производную от неё надо искать аккуратно.
Рассмотрим эту сложную функцию. Сначала была простая линейная функция

Потом её возвели в квадрат и получили новую функцию

А потом от этой новой функции, от v, взяли натуральный логарифм и получили уже третью функцию u(v)

И теперь, по правилам дифференциирования, чтобы найти производную функции u(x) надо перемножить

Сделаем такие действия с заданной в условии функцией

А в целом производная от суммы трёх слагаемых получится такая

2) Приравниваем производную к нулю и решаем полученное уравнение

Это ответ. Если бы уранение имело два или больше корней, нады бы было проверить, который из них является максимумом. А ещё бывают задания, типа "найти наибольшее значение функции". Тогда надо искать не икс, а игрек. Найти икс, подставить в исходную формулу и вычислить игрек. Так что, условия надо читать повнимательней.
|
|
|
-5 |
|
|
а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие промежутку 
|
|
|
Данное задание проверяет наше умение решать тригонометрические уравнения.
Простейшее тригонометрическое уранение выглядит например так sin x = 0 или так sin x = 1/2.
Неизвестная величина х - это угол, синус которого равен нулю (в первом случае) или 1/2 (во втором случае).
Мы имеем кое-какие представления о тргонометрии, и знаем, что sin 0 = 0. Получается х = 0. Это решение первого уравнения? Да, решение. Но не всё решение. Потому что

Уравнение имеет бесконечное множество корней, каждый из которых на "пи" отличается от другого. В общем виде корни уравнения принято записывать так

Множитель k принадлежит (значок, похожий на букву Е, означает "принадлежит") множеству целых чисел Z. То есть k может принимать любые целые значения {...-3, -2, -1, 0, 1, 2, 3, ...}.
Второе простейшее уравнение sin x = 1/2 тоже имеет множество корней. Не станем пояснять вывод формулы, его ты легко найдёшь в любом учебнике, сразу дадим формулу корней в окончательном виде

Но эти формулы позволяют решать простейшие уравнения, а у нас в исходных данных уравнение чуть более замысловатое. Поэтому его для начала надо максимально упростить. Вспомним формулы для двойного угла и основное тригонометрическое тождество. Считается, мы это должны помнить наизусть. И сделаем так:

А для правой части уравнения вспомним одну из формул приведения

Теперь заданное уравнение можем переписать в таком виде

И дальнейшие преобразования

Произведение двух сомножителей равно нулю, если хотя бы один из них (или оба) равны нулю. Наше уравнение распадается на два простейших

и

Оба эти простейших уравнения мы уже рассмотрели, решения их показали. и У того и того уравнения, как говорилось, корней бесконечное множество. А теперь надо выполнить задания б) выбрать из этого множества только те корни, которые принадлежат промежутку  . .

Промежуток я нарисовал на прямой, вообще-то надо рисовать круг. Подставляем в формулу

разные значения k. При k = - 2  Это единственный корень, который входит в заданный промежуток. Это единственный корень, который входит в заданный промежуток.
Затем, возьмём корни

и будем также подставлять вместо k разные значения. Найдём, что в заданном промежутке находятся корни

|
|
|
В данной задаче надо в бланк записывать не только ответ, но и выкладки.Ответ
а) : : 
б)  ; ;
|
|
|
|
|
![]()


.gif)

































.gif)





