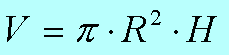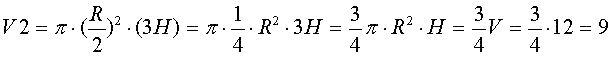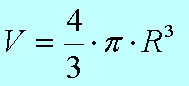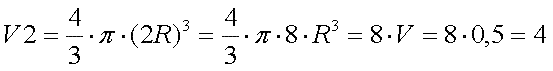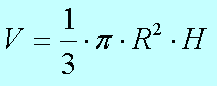WEB-РЕПЕТИТОР "ПОМОГАЛЫ"
Пособий для подготовки к ЕГЭ немало. Зачем же еще одно, на нашем сайте?
Наше "кредо" таково - растолковать решения экзаменационных заданий маскимально простым языком, без ненужного углубления в дебри, с набором самых простых и общеизвестных формул - но чтобы, тем не менее, абитуриент, готовящийся по нашему репетитору, мог набрать достойный балл для поступления в ВУЗ.
|

Пример В11 – 1
Объем первого цилиндра равен 12 куб.м. У второго цилиндра высота в 3 раза больше, а радиус основания в 2 раза меньше, чем у первого. Найдите объем второго цилиндра (в куб. метрах).
Решение. Цилиндр, как все мы хорошо знаем, это такое геометрическое тело типа банки из-под сгущенки. Сверху и снизу у него одинаковые основания – круглые. А расстояние между ними – высота. Банка от шпротов или кильки – это тоже цилиндр, только высота у них намного меньше сгущеночной.
Объём цилиндра вычисляется по формуле: Площадь основания умножить на высоту. В основании, как уже говорилось, КРУГ, площадь круга равна ПИ ЭР КВАДРАТ, поэтому подробная формула для вычисления объема цилиндра такая:
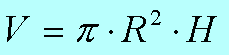
И вот по такой формуле мы, допустим, нашли объем первого цилиндра и определили, что V1 = 12.
А теперь согласно условию примем, что высота второго цилиндра в три раза больше, чем высота первого Н2 = 3Н, а радиус основания второго цилиндра в два раза меньше, чем радиус основания первого R2 = R/2
Тогда получится так:
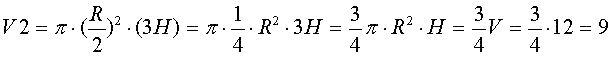
Ответ: 9
Пример В11 – 2
Бетонный шар весит 0,5 тонн. Сколько будет весить шар вдвое большего радиуса, сделанный из такого же бетона?
Решение: Я знаю такой банк, у них на крыльце по бокам как раз два здоровенных бетонных шара. В задаче сказано: из такого же бетона. Это следует понимать так: во сколько раз объем второго шара будет больше, во столько же раз и вес его будет больше.
Сперва напрягаем мозги и вспоминаем формулу объема шара.
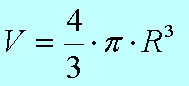
Затем поступаем, как в предыдущей задачке. Радиус второго шара R2 считаем в два раза большим, чем радиус R; R2 = 2R.
Тогда получится так:
Ответ: 4
А если я на ЕГЭ забуду формулу объёма шара? Всё, пипец? Не решить эту задачку?
Можно решить и без формулы. Если иметь в виду следующее соображение.
Длина – это линейная величина, измеряется в простых метрах или сантиметрах.
Площадь – это квадратная величина, измеряется в квадратных метрах или сантиметрах.
Объем – это кубическая величина, измеряется в кубических метрах или сантиметрах.
Поэтому, если радиус увеличить в 2 раза, то площадь увеличится в два в квадрате, то есть в 4 раза, а объем увеличится в два в кубе, то есть в 8 раз.
На эту тему – следующая задача.
Пример В11 – 3
Объем данного правильного тетраэдра 2 куб. см. Найдите объем правильного тетраэдра, ребро которого в 3 раза больше ребра данного тетраэдра.
Решение. Мы смутно помним, что за фигня такая – тетраэдр? Там еще вроде бы были октаэдр, икосаэдр, додекаэдр… Вроде как это геометрическое тело, составленное их четырех одинаковых правильных треугольников. А может и нет? И уж точно мы не помним формулу для объема этого тетраэдра!
Тем не менее, мы вполне осознаем, что длина ребра – это линейная величина, а объём – кубическая. При увеличении ребра в 3 раза, объём должен увеличиться в три в кубе раза, то есть в 3 на 3 на 3 = 27. Был объем 2 куб.см, увеличился в 27, получился 54.
Да, точно это правильный ответ.
Ответ: 54
Пример В11 – 4
Объём цилиндра равен 12 куб. см. Чему равен объем конуса, который имеет такое же основание и такую же высоту, как и данный цилиндр?
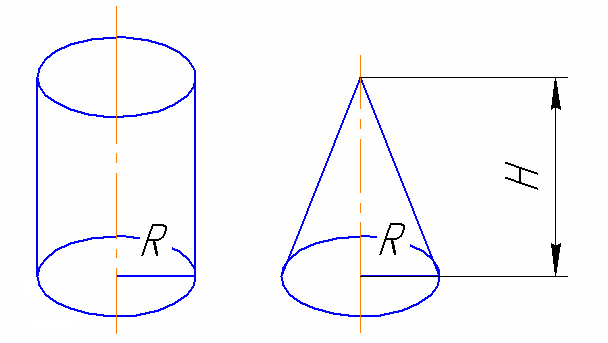
Решение. Здесь, конечно, без знания формул объема цилиндр и объема конуса обойтись невозможно. Про цилиндр мы уже говорили в примере В11 – 1; его объем находят по формуле
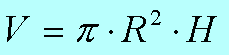
А объем конуса вычисляют по такой формуле:
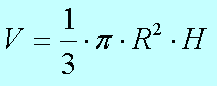
То есть объём конуса с таким же основанием и такой же высотой в ТРИ РАЗА меньше. 12 : 3 = 4.
Ответ: 4
Кстати говоря, есть хоть и не строгое, но любопытное доказательство формулы объема конуса. Делают, например из плотной бумаги, цилиндр и конус с одинаковым основанием и одинаковой высотой, как в условии этой задачи. А потом наливают в конус воду и переливают в цилиндр. Понадобится ровно, тютелька в тютельку, три конуса воды, чтобы наполнить цилиндр.
Пример В11 – 5
В цилиндрическом сосуде уровень жидкости достигает 384 см. На какой высоте будет находиться уровень жидкости, если её налить во второй сосуд, диаметр которого в 8 раз больше диаметра первого?
Решение: Диаметр больше в 8 раз = то и радиус (который равен половине диаметра) тоже больше в 8 раз. Площадь основания увеличится в 64 раза (восемь в квадрате), потому что площадь основания – это пи эр квадрат.
Но вода та же самая, объем жидкости не изменился при переливании. Поэтому, раз площадь основании увеличилась в 64 раза, то высота должна уменьшится во столько же раз, чтобы получить такой же объем.
Новая высота 384 : 64 = 6
Ответ: 6
Пример В11 – 6
В цилиндрический сосуд, в котором находилось 4 литра воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объём детали? Ответ выразите в литрах.
Решение. Задача на тему Архимеда и его знаменитого вопля «Эврика!». Помните эту историю? Какой-то их древнегреческий царь заказал корону из чистого золота и выдал мастеру нужное количество золота для работы. Вскоре корона (красивая!) была готова. Но царю нашептали, что мастер часть золота спёр, а заменил его серебром. То бишь корона не из чистого золота, а из сплава. Царь вызвал Архимеда и поручил проверить: так ли это? Архимед размышлял так. Вес короны известен. Плотность золота известна. Плотность умножить на объем – получится вес. Вроде всё просто. Если бы вместо короны был кубик золота, объём найти очень просто – измерить длину ребра и возвести в куб. Но корона весьма и весьма замысловатой формы. Всякие там завитушечки, листики, орнаментики и прочее. Как же определить объем такого фигуристого тела?
Думал Архимед – думал, думал-думал… И днем думал, и ночью думал. Всё никак не мог придумать. И вот решил он как-то принять ванну, и полез в неё, а она была наполнена до самых краёв. Вода, естественно, перелилась через край. Другой бы матюкнулся и взял тряпку. Но Архимед был философом. Почему вытекла вода? – подумал он. – Потому что моё тело, имея свой собственный объём, вытеснило сколько-то воды. А сколько именно? А ровно столько, каков объем моего тела. Значит, если в воду погрузить корону…
- Эврика! – закричал Архимед, что на древнегреческом означает «Нашёл!». Выскочил он из ванны, прямо в таком голожопом виде помчался по городу и вопил «Эврика!».
Правда история закончилась довольно печально. Мастера-ювелира уличили в воровстве и казнили.

К нашей задаче. Объём цилиндра линейно зависит от его высоты. Не квадратно, не кубично, а просто линейно. Высота увеличилась в 1,5 раз, значит и объём увеличился в полтора раза. Было 4 литра, стало 4 умножить на 1,5 = 6 литров. Добавилось 2 литра. Таков и есть объем погруженной детали.
Ответ: 2
Ролика подходящего не нашел, потом сам сделаю
 Назад к задаче В10 /Задача В11/ Вперед к задаче В12 Назад к задаче В10 /Задача В11/ Вперед к задаче В12
|
|
![]()